If you've done any 3d modeling before you may have heard that "You can't make a perfect sphere," since every 3d scene is just made of a bunch of triangles. But what if there is another way of doing 3d? Well there is: Ray marching and signed distance functions.

Ray marching renders 3d scenes by shooting rays (a line through space) towards the scene for each pixel and gathering data about where they hit. Instead of just checking for intersections with each object like in ray tracing, ray marching casts these rays by "marching" along them towards an object (the scene) defined by a function that returns the distance to it. The powerful part of a ray marcher is what you can do in and with this function:

Inside the function, you can create really neat things like fractals, twists, bends, and infinitely repeating objects at almost no extra computational cost, and using the function, you can quickly calculate soft shadows, ambient occlusion, and normals for any point in space.

And just to make this even better, it is incredibly easy to make a renderer for this function.

Throughout the first parts of this post, we will be working up to making some basic animations like this one:

In later parts (yet to be written), we will go over fractals and topics like ambient occlusion and soft shadows.

Note: I will never type out the full code for the ray marcher, but you can get to it at any point in this tutorial by hovering over a example window and clicking on the name.

Note #2: Although similar, ray marching, ray tracing, and ray casting are all slightly different. Ray casting typically casts along just one axis, ray tracing calculates intersections with each object directly using fancy math, and ray marching moves along a ray towards a scene defined by a signed distance function.

Building a Basic Ray Marcher

For now, we will make our ray marcher and scene entirely in a fragment shader written in GLSL on shadertoy.com. GLSL is the shader language used in OpenGL to give your triangles cool looks, but here we will be using it on two triangles that take up the whole screen. If you don't know what any of that means, just know that we will be building a function that is called for each pixel on the screen every frame and returns a color to be displayed.

I chose to use GLSL for this because it is what I learned, and it is easy to pick up just by looking at it, but a simple ray marcher can still be easily implemented in almost every language.

To start we will make this super simple animation of a sphere moving over a plane, which just casts a ray for each pixel and determines a shade of gray based on how far it goes:

To do this, we will need a rayMarch function which returns the distance a ray traveled before hitting the scene, and a function that returns the distance to the scene (we'll call this one getDistanceToScene)

Before we get to how the getDistanceToScene function works, lets make the rayMarch function.

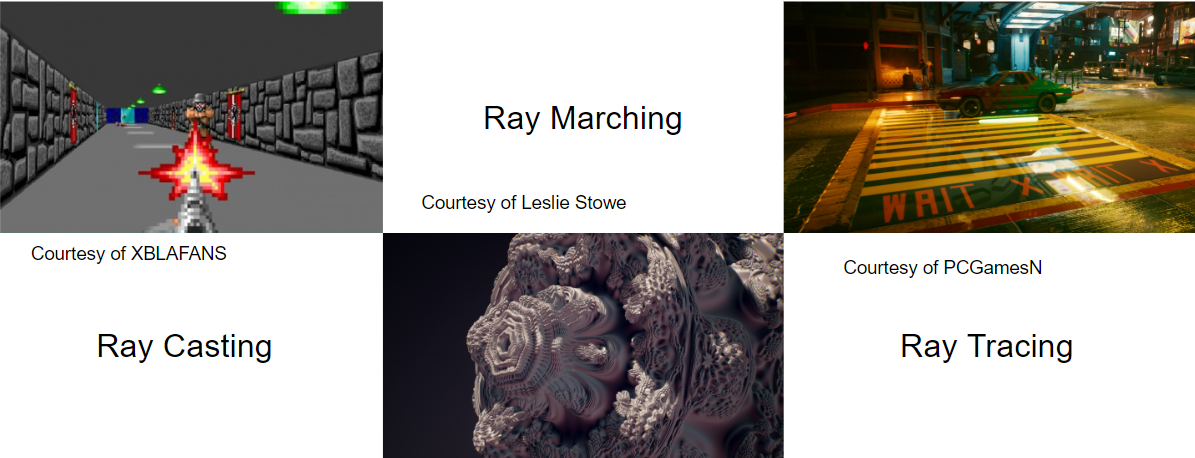
A ray marcher works by starting at a point, getting the distance to the scene, moving ("marching") along the ray by that distance to determine where it will sample from next, and repeating the cycle until the distance to the scene is 0 (or something like .01 to avoid it sampling forever when it gets close to an edge but doesn't hit it). That's it!

In this picture, the red line represents the ray and the grey circles and dark red points represent the samples. The gold star is where the ray marcher hit.

Our function can be implemented with:

#define MAX_MARCH_STEPS 100
#define MAX_MARCH_DIST 20.
#define MARCH_NEAR_DIST .01  // how close the ray can get to an object before counting it as a hit

float rayMarch(vec3 rayOrigin, vec3 rayDirection)
{
    float distanceFromOrigin = 0.;

    // march towards the scene in steps
    for (int i=0; i < MAX_MARCH_STEPS && distanceFromOrigin < MAX_MARCH_DIST; i++)
    {
        // calculate the next point to sample from
        vec3 point = rayOrigin + (rayDirection * distanceFromOrigin);

        float d = getDistanceToScene(point);
        distanceFromOrigin += d;

        // hit something 
        if (d <= MARCH_NEAR_DIST)
            return distanceFromOrigin;
    }

    // if it didn't hit anything
    return MAX_MARCH_DIST;
}

Simple right? We can render our scene by marching along a ray calculated as the direction through a camera and each pixel:

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // normalize pixel cordinates to -.5 to .5 on the y axis
    vec2 uv=(fragCoord.xy-.5*iResolution.xy)/iResolution.y;

    vec3 camera = vec3(0, 2, 0);
    vec3 rayDirection = normalize(vec3(uv.x,uv.y,1));

    float d = rayMarch(camera, rayDirection);

    // divide by MAX_MARCH_DIST for a fog effect
    fragColor = vec4(vec3(d/MAX_MARCH_DIST),1.0);
}

All we need to do now is make our function that returns the distance to the scene.

SDFs (signed distance functions)

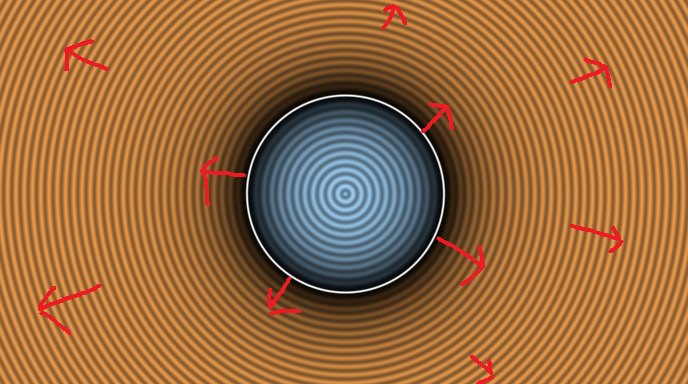
Signed distance functions do just what the name says they do: They are functions that return the distance to something from a point, being positive if it's outside, 0 if it's on the surface, and negative if it's inside. This is explained by this visual made by Inigo Quilez, the co-creator of shadertoy.com:

This represents the signed distance function for a 2D circle with blue showing negative values, and orange showing positive values.

To start, lets make the SDF for the ground.

This is probably the most simple SDF as it's just the distance of the sampling point's y value from the y value of the plane. This can be represented as abs(p.y - y) where p is the sample point and y is the location of the plane.

float planeSDF(vec3 p, float y)
{
    return abs(p.y - y);
}

We can now build the start of our getDistanceToScene function:

float getDistanceToScene(vec3 p)
{
    float ground = planeSDF(p, -1.);

    return ground;
}

To make an SDF for a sphere, all we need is to get the distance from the center of the sphere to the sample point, and subtract the radius. This makes all distances inside of the sphere negative, and keeps the distances greater than the radius positive.

float sphereSDF(vec3 p, float radius, vec3 position)
{
    return length(p-position) - radius;
    // same as distance(p,position) - raduis, but using this instead becomes important later
}

float getDistanceToScene(vec3 p)
{
    float sphere = sphereSDF(p, 2., vec3(-3,1,8));

    return sphere;
}

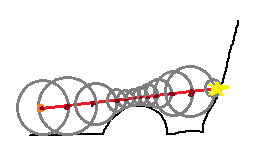
That's cool, but how do we combine the sphere and the plane?

Union SDF

If you have the result of two distance functions, how do you tell which is closer? You just take the smaller value! Remember, for now, all our ray marcher needs is the closest distance to the scene. It doesn't care about anything else.

We can implement this with the very short unionSDF function:

float unionSDF(float a, float b)
{
    return min(a,b);
}

Here is the completed code for our getDistanceToScene function with our fancy new unionSDF:

float sphereSDF(vec3 p, float radius, vec3 position)
{
    return length(p-position) - radius;
}

float planeSDF(vec3 p, float y)
{
    return abs(p.y - y);
}

float unionSDF(float a, float b)
{
    return min(a,b);
}

float getDistanceToScene(vec3 p)
{
    float ground = planeSDF(p, -1.);
    float sphere = sphereSDF(p, 2., vec3(-3,1,8));

    float scene = unionSDF(ground, sphere);

    return scene;
}

We can also add a little animation to our sphere by making it revolve in a circle:

    float sphere = sphereSDF(p, 2., vec3(
        1. * sin(iTime),        // x
        1,                      // y
        11. + 3. * cos(iTime)   // z
    ));

And that's it! Now you have everything you need to make a ray marcher. In the rest of this post, we will just be adding to this, with lighting, colors, and repetition, and other cool effects, but all of those are just additions, and now you already have your own working ray marcher.

Here's a great list of many 3d SDFs for common shapes and operators that can be used with them: https://iquilezles.org/articles/distfunctions/

Adding Color

Now that we have a basic ray marcher, we will add color to each object in our scene. This is a lot easier to do than it sounds because of how the rest of the ray marcher was set up. While it is easy to change the color of everything in our scene, the only challenge is how we differentiate between objects, as the ray marching function sees the scene as is a single object.

Luckily, In our unionSDF and getDistanceToScene functions, we are already differentiating between objects when we join them by taking the minimum distance. This means that if we tie some more data to the distance returned by each individual object's SDF, we can still easily differentiating which object is closer by just looking at the distance.

To implement this, we can create a struct for data about the closest surface and add more values, such as color:

struct closestObject {
    float d; // the distance to the surface
    vec3 col;
};

Note: When I wrote all of the code for this article, I used closestObject, but thinking back, a better name would have been closestSurface, as it does not give any identifying information about the object

Now that we're working with more values on top of the distances, we have to change how we get the closest object to make sure that any other data is also passed through. We can change our unionSDF function to unionObject:

closestObject unionObject(closestObject a, closestObject b)
{
    if (a.d < b.d) // min
        return a;
    return b;
}

Next, we'll have to update our getDistanceToScene to include color values when we define the objects, and rename it to getClosestObject:

closestObject getClosestObject(vec3 p)
{
    closestObject ground = closestObject(
        planeSDF(p, -1.), 
        vec3(0,1,1) // cyan
    );
    closestObject sphere = closestObject(
        sphereSDF(p, 2., vec3(-3.,1,9.)),
        vec3(1,0,0) // red
    );

    closestObject scene = unionObject(ground, sphere);

    return scene;
}

Note: One cool thing about getting the color in the getClosestObject function is that you can make it change depending on where the point is. This is how I made the checkerboard pattern in the first example, and how you could map textures onto surfaces. I might write a separate article about this in the future.

We have to update our rayMarch function to only use the distance value, and not the color:

    ...
    float d = getClosestObject(point).d;
    ...

In our main function we need just a few lines that calculate the point where the ray hit and one that gets that point's color:

    ...
    float d = rayMarch(camera, rayDirection);
    vec3 hitP = camera+rayDirection*d;

    vec3 col = getClosestObject(hitP).col;
    ...

We can also multiply our color by one minus the distance we had earlier for a fog effect:

    ...
    fragColor = vec4(col*vec3(1.-d/MAX_MARCH_DIST),1.0); // fog
}

Although you can tell what's happening in the render, it looks a bit flat. In the next part, we will be adding some basic lighting.

Fake Lighting

Lighting is one of the most important and complicated part of any 3D renderer. For now, we will just implement some basic lighting without any shadows.

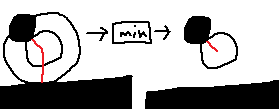
To calculate how bright a surface should be relative to an incoming light ray, we can use a little trick to quickly and easily get this value.

All we have to do is look at the angle that the light ray is hitting the surface. If the ray is hitting it head on, then it should be bright. If it's hitting it at an angle of 90 or greater, it shouldn't be lit up at all.

Instead of finding an actual angle, we can simply use the dot product of the light ray and the normal of the surface. This is fairly easy to implement, and a calculation of surface normals can be very helpful later on.

This dot product trick works as the dot product of two vectors is equal to the product of both of the magnitudes of both vectors (which are both just one as they are normalized) and the cosine of the angle in between them (1 when parallel or head on and 0 when perpendicular). It is also simply equal to A_x*B_x + A_y*B_y + A_z*B_z where A and B are the two vectors making it a very simple and fast operation.

In this MS paint visual, I wrote out the dot products of the light rays and surface normals. Any of the dot products on the unlit side will be negative and should be clamped to 0 because you can't have a negative amount of light (this matters if you have multiple light sources).

Normals

Normals are the perpendicular vectors coming off of a surface. With scenes defined by SDFs, you can get a normal for any point in space.

To find the normal of a point, you find the difference between a vector made up of the distances to the scene from an offset point in each direction (dx, dy, dz) and the original sample point (x, y, z). This is a bit confusing, but all it does is build a new vector representing the amount of change in each direction, I believe that is is similar to a gradient in math.

This can be implemented in 3d using:

vec3 getNormal(vec3 p)
{
    vec2 e = vec2(.01,0); // used to build translation vectors like e.xyy=vec3(.01,0,0)

    vec3 n1 = vec3(
        getClosestObject(p+e.xyy).d, // x offset
        getClosestObject(p+e.yxy).d, // y offset
        getClosestObject(p+e.yyx).d  // z offset
    );

    return normalize(n1-getClosestObject(p).d);
}

We can get a little more precision by also sampling points in the opposite direction, but this is not 100% necessary:

// extra precision
vec3 getNormal(vec3 p)
{
    vec2 e = vec2(.01,0);

    vec3 n1 = vec3(
        getClosestObject(p+e.xyy).d,
        getClosestObject(p+e.yxy).d,
        getClosestObject(p+e.yyx).d
    );
    vec3 n2=vec3(
        getClosestObject(p-e.xyy).d,
        getClosestObject(p-e.yxy).d,
        getClosestObject(p-e.yyx).d
    );

    return normalize(n1-n2);
}

Sorry if this is a bit confusing, you don't really need to know how it works (I didn't until I wrote this), but just know that it works fairly well (but not perfect, smaller values of e will provide higher accuracy).

Lighting Implementation

Before we go on, lets increase how far we can see to better demonstrate the light hitting the ground:

#define MAX_MARCH_STEPS 200
#define MAX_MARCH_DIST 250.
#define MARCH_NEAR_DIST .01

We can easily write our getLighting function using the method described earlier:

vec3 getLighting(vec3 p)
{
    vec3 col = getClosestObject(p).col;

    vec3 lightRay = normalize(vec3(1,1,-.5)); // the direction that light comes in from
                                              // try playing around with this vector

    float lighting = clamp(dot(lightRay, getNormal(p)), 0., 1.); // don't forget to round out the negatives

    return col*lighting;
}

In our main function we have to replace our old method of just getting the color directly from the scene with our new getLighting function.

    ...
    vec3 col = getClosestObject(hitP).col; // OLD
    vec3 col = getLighting(hitP);          // NEW

    fragColor = vec4(col*vec3(1.-d/MAX_MARCH_DIST),1.0); // we can keep the distance fog
}

If we want to use a point light instead of the global lighting, all we need to change is how we calculate our light ray:

    vec3 lightPos = vec3(0, 3, 5. + sin(iTime) * 5.); // a bit of motion on the z axis
    vec3 lightRay = normalize(lightPos-p);

One of the nice things about building something from scratch is that you have complete control over everything. For example if I wanted to give the scene some cartoony lighting all I'd need to do is use a ceiling function (round up) with a multiplied version of the lighting value and shrink it back down:

        lighting = ceil(lighting*5.)/5.;

Now that our scene looks partly presentable, we can start talking about the cool parts of what we can do with SDFs. 😎

Transformations & Intro to Cool Functions

Left - translation, center - scale, right - rotation

Transformation with SDFs works a bit different than you may think: Instead of moving the object, you move the point being sampled.

This idea of moving the point in space is already demonstrated in our sphereSDF function:

float sphereSDF(vec3 p, float radius, vec3 position)
{
    return length(p-position) - radius;
}

We can move the -position from inside the function to outside of the function when we call call it:

float sphereSDF(vec3 p, float radius)
{
    return length(p) - radius;
}

sphere = sphereSDF(p - position, 2.) // moved the translation

Our SDF can now assume the center should always be at the origin (0, 0, 0), which makes things much easier when writing it.

We can rewrite all of our SDFs to work around the origin, making them simpler and avoiding repetitive code:

// simpler SDFs 
float sphereSDF(vec3 p, float radius)
{
    return length(p) - radius;
}

float planeSDF(vec3 p)
{
    return abs(p.y); // distance to y=0 (definition of absolute value)
}

And we can define translations for our objects in the getClosestObject function:

closestObject getClosestObject(vec3 p)
{
    closestObject ground = closestObject(
        planeSDF(p - vec3(0,-1,0)), // move to (0, -1, 0)
        vec3(0,1,1)); // color

    closestObject sphere = closestObject(
        sphereSDF(
            p - vec3(sin(iTime)*7., 1, 15),  // slide between (-7, 1, 15) and (7, 1, 15)
            2.),      // radius
        vec3(1,0,0)); // color

    closestObject scene = unionObject(ground, sphere);

    return scene;
}

Although this does the exact same thing as having our positions separate in the function arguments, it's better because now we don't have to put those in every SDF which will also allows us to make new transformations that work on any object.

For example, to scale any SDF we can use:

object = mySDF(p / scale) * scale

We can also do rotation on any point, but this is a lot harder and I'm not going to go into how it works. Here's a basic rotation function which takes a point and a vector of pitch, roll, and yaw in Euler angles (degrees) as its arguments:

vec3 rotate(vec3 p, vec3 rot)
{
    rot = mod(rot, 360.)/(180./3.1415); // degrees to radians

    float ca = cos(rot.x); float sa = sin(rot.x);
    float cb = cos(rot.y); float sb = sin(rot.y);
    float cy = cos(rot.z); float sy = sin(rot.z);

    return p*mat3(
        cb*cy         , cb*sy         , -sb,
        sa*sb*cy-ca*sy, sa*sb*sy+ca*cy, sa*cb,
        ca*sb*cy+sa*sy, ca*sb*sy-sa*cy, ca*cb
    );
}

This function is taken from Wikipedia.

Other functions?

So now we know what happens when we use basic functions like subtraction/multiplication, but what happens when you use more complicated functions? Lets try putting our sample point into a modular system:

closestObject getClosestObject(vec3 p)
{       
    closestObject spheres = closestObject(
        sphereSDF(
            mod(p, vec3(4)) - vec3(2), // -vec(2) to include negatives
            1.),
        vec3(1,0,0) // red
    );

    return sphere;
}

Note: If you are making this yourself, you might need to move the camera out of a sphere.

Wow! All we added is one extra cheap operation into our function and now there's an infinite amount of spheres! What happened?

It's really simple: When we put each value of the point into a modular system of 4 (mod(p, vec3(4))), it made the point "repeat" every 4 units over and over. I also had to subtract 2 to make sure the result of the modulus included negatives.

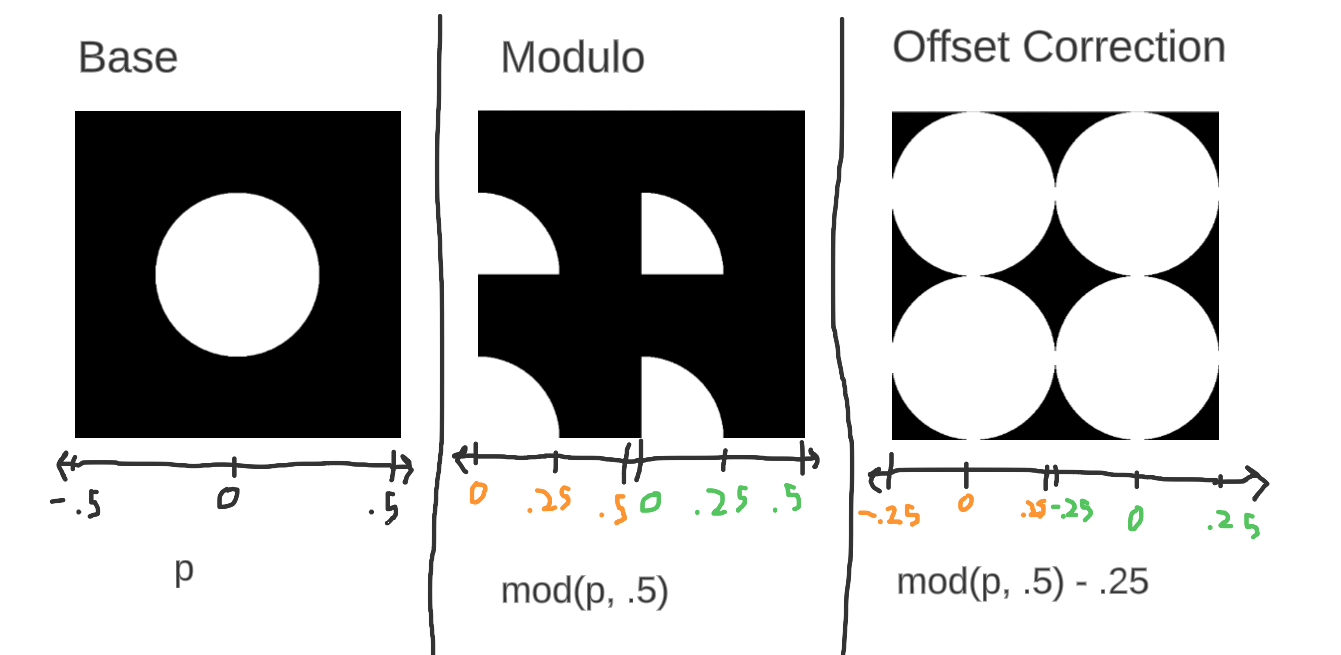
Note: Although this works great if every repeated cell is the same, it breaks a bit if the cells are different. Inigo Quilez has a great article on this and how to fix it at: https://iquilezles.org/articles/sdfrepetition/

This is barely scratching the surface of what you can do, so I encourage you to try some of this out, research a bit, and just have fun with it.

Some other cool things to research or play with are: - Shadows (simplest way is just casting a ray from surface point to light source and seeing if it hits anything) - Soft shadows - Smooth unions and other cool sdf funcitons (good resource: https://iquilezles.org/articles/raymarchingdf/) - Volumetrics (fog/clouds or even grass) - Ambient occlusion - Noise - Procedural textures